The general solution of the equation $\sin^2 \theta \sec\theta \sqrt{3} \tan \theta = 0$ is0911 · In mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometricThe Unit Circle and The Angle (Part 1 of 2) The Unit Circle and The Angle (Part 2 of 2) The Unit Circle and The Angle (30 and 60 Degrees) The Unit Circle and The Signs of x and y;

1 Example 6 1 Prove That Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta
Simplify (1+tan^(2)theta)sin^(2)theta
Simplify (1+tan^(2)theta)sin^(2)theta-`tan^2 theta 1 = 1/(cos^2 theta)` which gives `tan^2 theta 1 = sec^2 theta` Approved by eNotes Editorial Team We'll help your grades soar Start your 48hour free trial and unlock all the0812 · Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities Trigonometric Identities With Examples Example 1 Prove the following trigonometric identities (i) (1 – sin 2 θ) sec 2 θ = 1 (ii) cos 2 θ (1 tan 2 θ



Trigonometry 1
I want to use the fact that sin(2θ) = 2tan(θ) 1 tan2(θ) to solve sin(2θ) − tan(θ) = 0 for 0 ≤ θ ≤ 2π My solution 2tan ( θ) 1 tan2 ( θ) − tan(θ) = 0 so 2tan ( θ) − ( 1 tan2 ( θ)) tan ( θ) 1 tan2 ( θ) = 0 so 2tan(θ) − (1 tan2(θ))tan(θ) = 0LHS, = ( sec^2θ tan^2θ)/sinθ = 1/sinθ = cosecθ ** we know , the formula of sec^2θ – tan^θ =1 , which can be easily found by putting secθ = 1/cosθ and tanθ = sinθ/cosθ · 1 – sin 2 θ = cos 2 θ √a 2 x 2 x = a tan θ 1 – tan 2 θ = sec 2 θ √x 2 − a 2 x = a sec θ sec 2 θ – 1 = tan 2 θ
Verify 2tan (theta)/1tan^2 (theta) = sin2 (theta)Integrate sin^2(theta) Extended Keyboard;Use identity sin^2 theta cos^2 theta = 1 to prove sec^2 theta = 1 tan^2 theta Browse by Stream Engineering and Architecture
Siyavula's open Mathematics Grade 11 textbook, chapter 6 on Trigonometry covering Trigonometric identitiesWe see that the graph of \(Y_1 = \cos^2 \theta \sin^2 \theta\) appears identical to the horizontal line \(Y_2 = 1\text{}\) In fact, the graphs are identical, and the equation \(\cos^2 \theta \sin^2 \theta = 1\) is an identity It is important enough to earn a special name Pythagorean Identity For any angle \(\theta\text{,}\)L H S = tan 2 θ − sin 2 θ = cos 2 θ sin 2 θ − sin 2 θ = sin 2 θ (sec 2 θ − 1) = sin 2 θ tan 2 θ = R H S



1 1 Tan 2 Theta 1 1 Cot 2 Theta 1 Sin 2 Theta Sin 4 Theta Brainly In
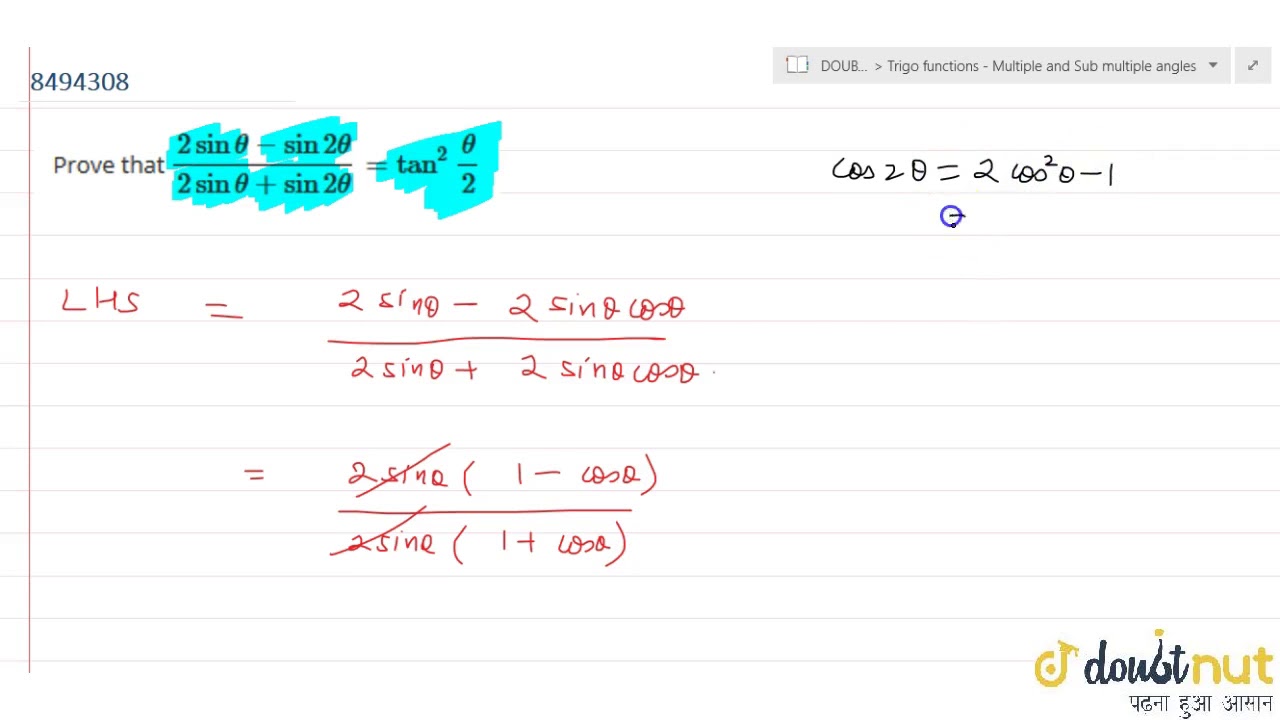


Prove That 2 Sin Theta Sin 2theta 2 Sin Theta Sin 2theta Tan 2 Theta 2 Youtube
How do you prove that #sec xcot x = csc x#?Thanks Found 2 solutions by stanbon, solver Answer by stanbon(757) (Show Source) You can put this solution on YOUR website!5 x = c o s − 1 ( 1 1 t 2),y = s i n − 1 ( 1 1 t 2) t h e n d y d x is equal to VITEEE 09 6 The value of c in Lagrange's theorem for the function f ( x) = log ( sin x) in the interval π 6, 5 π 6 is



3 4sin 28 Cos 28 3 Tan 28


Evaluate Cosec 2 90 8 Tan 2 8 4 Cos 2 40 Cos 2 50 2 Tan 2 30 Sec 2 52 Sin 2 38 3 Cosec 2 70 Tan 2 Sarthaks Econnect Largest Online Education Community
Is true for #(5pi)/6#?I'm going to use the double angleProve that Sin(theta)times Cos(theta) divided by Cos^2(theta)Sin^2(theta)=Tan(theta) divided by 1Tan(theta) Show step by step how to change the left to equal the right side of equasion This question is from textbook Algebra and Trigonomometry Answer by jim_thompson5910() (Show Source) You can put this solution on YOUR website!



The Allowed Values For Sin 2 8 Pmns 13 As A Function Of Tan 2 8 Vm 23 Download Scientific Diagram


Prove 1 Tan 2 Theta Sec 2 Theta Mathematics Stack Exchange
Approach 1 Starting with the left hand side We can rewrite \(\sin\theta\) by using the double angle formula \\sin\theta= \sin\bigl(2(\tfrac{1}{2}\theta)\bigr)= 2Question How to simplify tan^2 theta/sin^2 thetado I plug in the sin/cos for tan and csc for sin?2 tan theta /(1 tan^2 theta) = sin 2theta Hi Charmaine, In a problem like this when I don't immediately see something useful I write everything in terms of sines and cosines and then see if I can manipulate both sides to make them equal In this case replace tan(θ) by sin(θ) /cos(θ) and sin(2 θ) by 2 sin(θ) cos(θ) Penny Math Central is supported by the University of Regina and



Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Tan 2 Theta Sin 2 Theta Sin 4 Theta Sec 2 Theta
Nghi N Dec 18, 15 f (x) = sin4x −cos2x− tan2x = = (sin2x−cosx)(sin2x cosx)− cos2xsin2x It is given (\tan \theta 1) (\sin^² \theta 3\cos^² \theta)=0, find the possible values of \tan \theta It is given (tanθ 1)(sin² θ −3cos² θ)= 0, find the possible values of tanθ https//mathstackexchange · Explanation (1 tan2(θ))(cos2(θ)) = ( cos2(θ) cos2(θ) sin2(θ) cos2(θ))(cos2(θ)) = ( cos2(θ) sin2(θ) cos2(θ))cos2(θ) = ( 1 cos2(θ))cos2(θ) = 1 using cos2(θ) sin2(θ) = 1Simplify tan^2 theta/sin^2 theta= sin^2/cos^2/sin^2 Invert the denominator and cancel= sin^2/cos^2= 1/cos^2 = sec^2(theta



Prove The Identity Sin 2 Theta 2 Tan Theta Sin Theta 2tan Theta Study Com



Sin Theta Sin 2 Theta 1 Cos Theta Cos 2 Theta Tan Theta Prove Brainly In
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge andThe Trigonometry Function Sine Explained;In the expression for sin 2, n must be at least 1, while in the expression for cos 2, the constant term is equal to 1 The remaining terms of their sum are (with common factors removed) = = () = = () = = by the binomial theorem Consequently, = , which is the Pythagorean trigonometric identity When the trigonometric functions are defined in this way, the identity in combination



Cos2 Theta Tan2 Theta 1 Sin2 Theta Tan2 Theta Brainly In



1 Example 6 1 Prove That Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta
Join for Free Problem (a) Choose (at random) an angle $\theta$ such tha 0242 View Full VideoIf a \sin ^{2} \thetab \cos ^{2} \theta=1, show that \sin ^{2} \theta=\frac{1b}{ab} \quad \text { and } \quad \tan ^{2} \theta=\frac{b1}{1a} Our Discord hit 10K members!How do you show that #2 \sin x \cos x = \sin 2x#?


Solved Cot 2 Theta Tan 2 Theta Sec 2 Theta Csc2 Theta Chegg Com


Solution Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta
0121 · The LibreTexts libraries are Powered by MindTouch ® and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot We also acknowledge previous National Science Foundation support under grant numbers ,1800 · So I get that $$ \sin 2 \theta=\frac{4}{5} $$ $$ \cos 2 \theta=\frac{3}{5} $$ But what is the next step?2218 · Find an answer to your question prove that tan2 theta/tan 2 theta1 cosec 2 theta/sec 2 theta cosec 2 theta =1/sin 2 theta cos2 theta


The Trigonometric Ratios Of Angl


Cos Theta 4 5 0 Theta 90 Use The Information En Ya Guru
How do you prove that #cos 2x(1Stress Transformation General Stress State The general state of stress at a point is characterized by three independent normal stress components and three independent shear stress components, and is represented by the stress tensorThe combination of the state of stress for every point in the domain is called the stress fieldSolutionShow Solution Given θ = 30° (1) To veriy `sin 2theta = (2 tan theta)/ (1 tan^2 theta)` (2) `sin 2 theta = sin 2 xx 30` = sin 60 `= sqrt3/2`



Tan 28 Sin 28 Sin 48sec 28



Double Angle Identities Trigonometry Socratic
In this video I will solve tan^2(theta)4=0, theta=?Prove\\tan^2 (x)\sin^2 (x)=\tan^2 (x)\sin^2 (x) \frac {d} {dx} (\frac {3x9} {2x}) (\sin^2 (\theta))' \sin (1) \lim _ {x\to 0} (x\ln (x)) \int e^x\cos (x)dx \int_ {0}^ {\pi}\sin (x)dx \sum_ {n=0}^Course Index What Is The Unit Circle?



If Tan Theta 3 4 Then Find The Value Of Cos2 Theta Sin2 Theta Maths Introduction To Trigonometry Meritnation Com



Solve Sin 2thetacos 2theta Sin 2theta1 Tan 2theta Sin 2theta
The Trigonometry Function Cosine Explained; · How do you prove #\csc \theta \times \tan \theta = \sec \theta#?How do you prove #(1\cos^2 x)(1\cot^2 x) = 1#?



Why Do We Divide A B Absin Theta In A B Abcos Theta For Finding The Angle Between Them Quora



Trigonometry 1
If `tan\ theta/2=(cosec thetasin theta),` then `tan^2\ theta/2` may be equal to (A) `2sqrt(5)` (B) `(94sqrt(5))(2sqrt(5))` `2sqrt(5)` (D) `(94sqrt · Trigonometric Identities Basic Definitions Definition of tangent $ \tan \theta = \frac{\sin \theta}{\cos\theta} $ Definition of cotangent $ \cot \theta = \frac{\cos(\sin^2(\theta))'' \frac{d^2}{dy^2}(a^y) \frac{d^2}{dx^2}(\frac{\sqrt{x}}{2x3}) \frac{d}{dx^2}(e^{x^n}) (x\ln(x))''



Ex 6 1 Q Tan 2theta Sin 2theta Tan 2theta Sin 2theta Prove The Following



Tangent Half Angle Formula Wikipedia
🎉 Meet students and ask top educators your questionsJoin Here!Answer to Find the exact value of sin (2 theta), cos (2 theta), tan (2 theta), and the quadrant of 2 theta sin (theta) = {square root {10}} /0121 · Using \(3\theta = 2\theta \theta \), the addition Equation for sine, and the doubleangle Equations \ref{eqndoublesin} and \ref{eqndoublecosalt2}, we get


If Tan 2theta 1 2tan 2a Then Prove That 2sin 2theta 1 Sin 2a Mathematics Topperlearning Com 47



Worksheet On Finding The Unknown Angle Using Trigonometric Identities
Explanation \displaystyle{{\tan}^{{2}}\theta}{1}={4}{2}{\tan{\theta}} \displaystyle{{\tan}^{{2}}\theta}{2}{\tan{\theta}}{3}={0} Use the pythagorean identity tan 2 θ 1 = sec 2 θ Explanation tan 2 θ 1 = 4 − 2 tan θ tan 2 θ 2 tan θ − 3 = 0Proofs of trigonometric identities are used to show relations between trigonometric functionsThis article will list trigonometric identities and prove themProve that tan^2 theta sin^2 theta = tan^2 theta sin^2 theta


Tinkutara Equation Editor Math Forum Question 8176



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
Verify the fundamental trigonometric identities Identities enable us to simplify complicated expressions They are the basic tools of trigonometry used in solving trigonometric equations, just as factoring, finding common denominators, and using special formulas are the basic tools of solving algebraic equationsSolutionShow Solution LHS = `tan^2 theta sin^2 theta = sin^2 theta/cos^2 theta sin^2 theta` ` ∵ tan^2 theta = sin^2 theta/cos^2 theta` Is there an error in this question or solution?Find the exact value of $\sin 2 \theta, \cos 2 \theta, \tan 2 \theta,$ and the quadrant in which $2 \theta$ lies $$ \cos \theta=\frac{5}{13}, \theta \text { in quadrant } I $$



Small Angle Approximation Wikipedia



Solved Find The Exact Value Of Sin 2 Theta Co


How I Remember Trig Identities Part 2 Beyond Solutions



If Theta 30 Verify That I Tan2theta 2tantheta 1 Tan 2theta Ii Sin2theta Youtube



If Tan Theta 2 Cosec Theta Sin Theta Then Tan 2 Theta 2 May Be Equal Youtube



Solve Sin 2 Theta Tan Theta Cos 2 Theta Cot Theta Sin 2 Theta 1 T
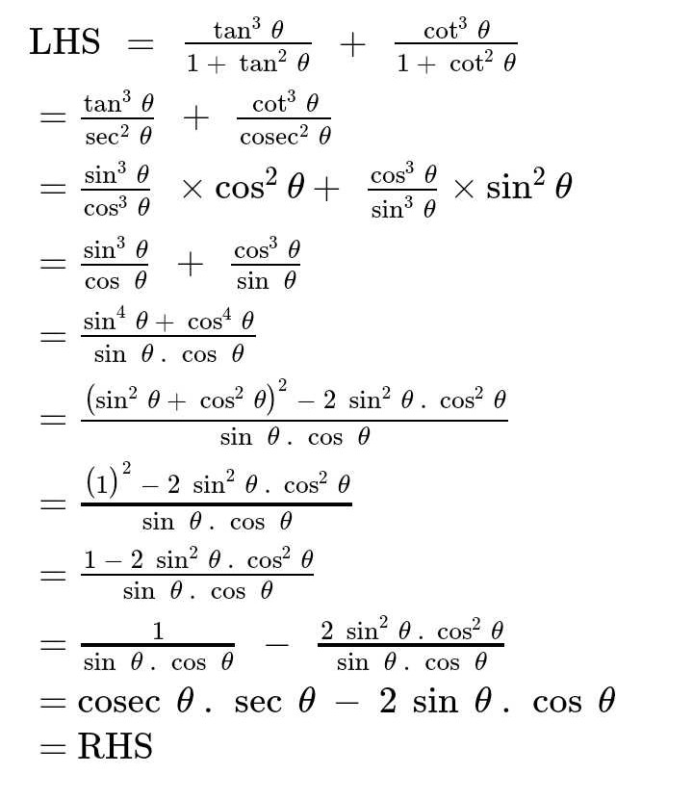


Prove If Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Cosec Theta 2 Sin Theta Cos Theta Edurev Class 10 Question
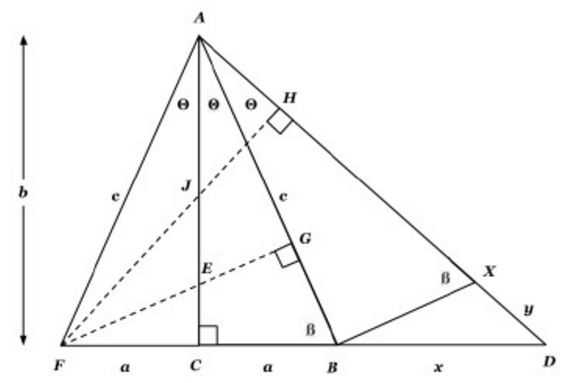


Much From Little



Get Answer Prove The Given Identity Cos 2 Theta 1 Tan2 Theta 1 Which Transtutors
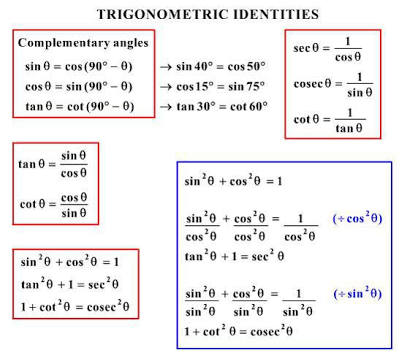


How Do You Simplify The Expression Sin 2theta Cos 2theta Cos 2theta Socratic



Solved Which Expression Is Equivalent To Tan 2 Theta Si Chegg Com



If Cot Theta 12 5 Show That Tan 2 Theta Sin 2 Theta Sin



Prove That Tan2 Theta Sin2 Theta Tan2 Theta Sin2 Theta Brainly In


How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic


1 Sin2 Theta 3 X Sin Theta X Cos Theta Introduction To Trigonometry Maths Class 10



View Question Sin 2 Theta Cos Theta Tan Theta Sin Theta



Prove That Tan Theta Cot Theta 2 Sin2 Theta Son Theta Cos Theta 1 2 Cos2 Theta Maths Introduction To Trigonometry Meritnation Com



Trigonometric Identities Topics In Trigonometry
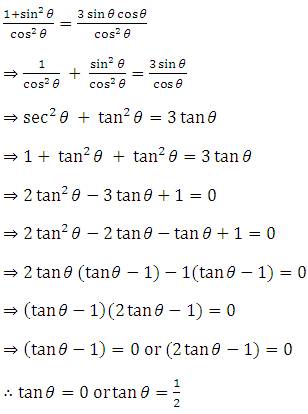


1 Sin2 Theta 3 X Sin Theta X Cos Theta Introduction To Trigonometry Maths Class 10



Tangent Half Angle Formula Wikipedia



Tangent Half Angle Formula Wikipedia
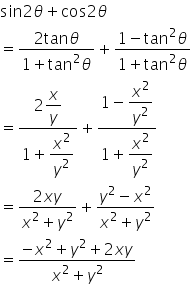


If Tan Theta X Y Then Find Sin 2 Theta Cos 2 Theta Mathematics Topperlearning Com 3co7touu



If 8 Is An Acute Angle And Sin 8 Cos 8 Then The Value Of 2 Tan 2 Theta Cos 2 Theta 2 Is Snapsolve



स द ध क ज ए Sin 2theta 1 Cos 2theta Tan Theta Youtube



Prove That Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange



Solved Prove The Following Identities Tan 2theta 2 Tan Chegg Com



Ii Sin 0cot2 0 Cos 0tan 0 1 See How To Solve It At Qanda



7 6 Double Angle Half Angle Formulas Flashcards Quizlet



The Allowed Values For Sin 2 8 Pmns 13 As A Function Of Tan 2 8 Vm 23 Download Scientific Diagram



Cos Squared Theta Minus Sin Square Theta Equal To 1 Minus 10 Squared Theta By 1 10 Squared Theta Prove The Identity Class Of Achievers



The Number Of Roots Of The Equation Left 1 Tan Theta Right Left 1 Sin2 Theta Right 1 Tan Theta Theta In 0 2 Pi Is A 3 B 4 C 5 D None Of These Snapsolve



Prove That Sec 4 Theta 1 Sin 4 Theta 2 Tan 2 Theta 1 Maths Introduction To Trigonometry Meritnation Com


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora



If 2 Sin 2 Theta 5sin Theta 3 0 Then Find The Value Of Tan 4 Theta Tan 2 Theta 9 Youtube



Tan 2theta Sin 2theta Tan 2theta Sin 2theta


Solution Prove Sin 2theta 2tan Theta 1 Tan 2 Theta


Prove Tan 2 8 Sin 2 8 Tan 2 8 Sin 2 8 Sarthaks Econnect Largest Online Education Community
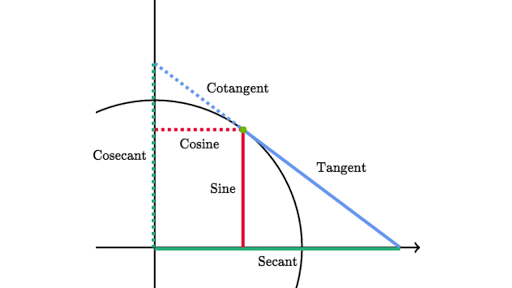


Trig Identity Reference Article Khan Academy



Solved Does Tan 2 Theta Frac Sin 2 Theta C



Prove That Tan Squared Theta Minus Sin Square Theta Sin Square Theta Tan Square Theta Maths Introduction To Trigonometry Meritnation Com



Tan 2theta Sin 2theta Tan 2thetasin 2theta



Prove That A Sin 2 Theta 1 Cos 2 Theta Tan Theta B 1 S



If Tan Theta A B Then What Is The Value Of Sin 2 Theta Cos2 That Tan 2 Theta Quora
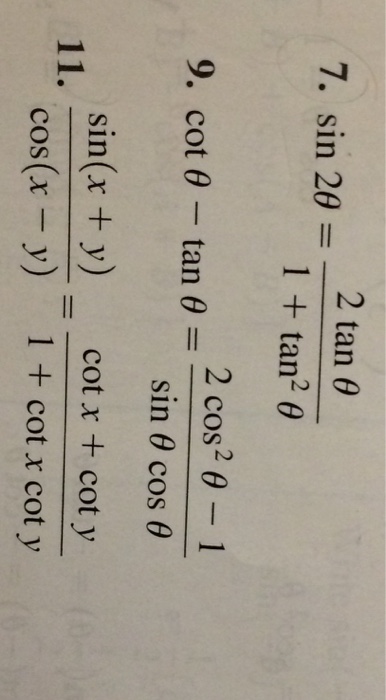


Solved Sin 2 Theta 2 Tan Theta 1 Tan 2 Theta Cot Thet Chegg Com
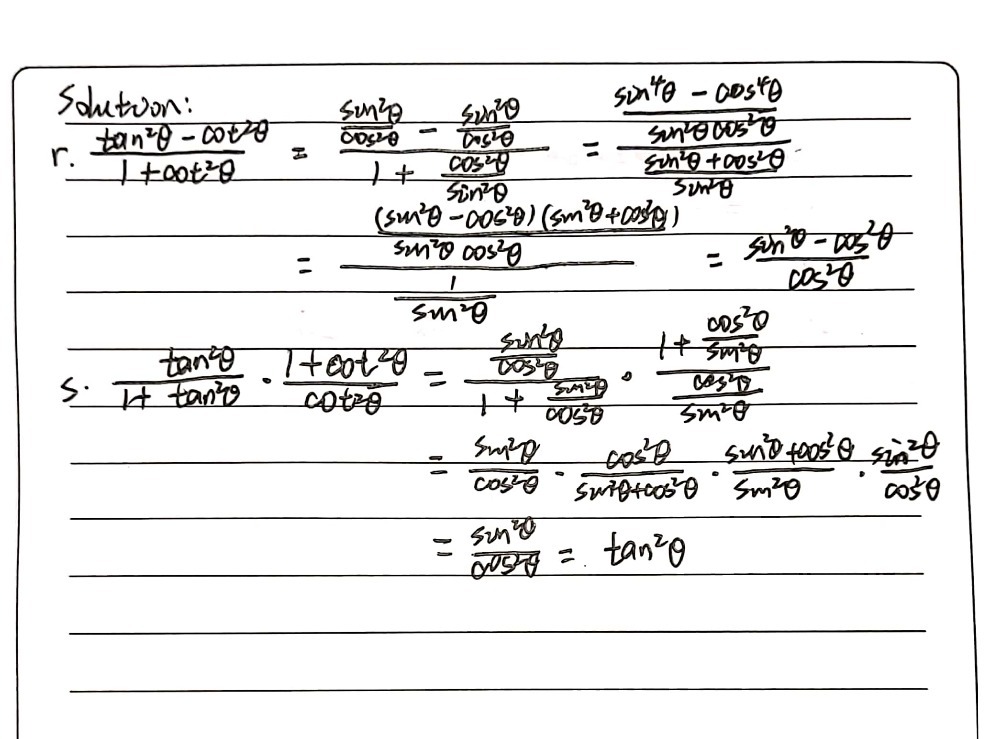


Bysyyapnuctm5m


The Trigonometric Ratios Of Angl



Please Answer My Question Fast Please If Theta 30 Degrees Verify That 1st Question Sin 2theta Brainly In
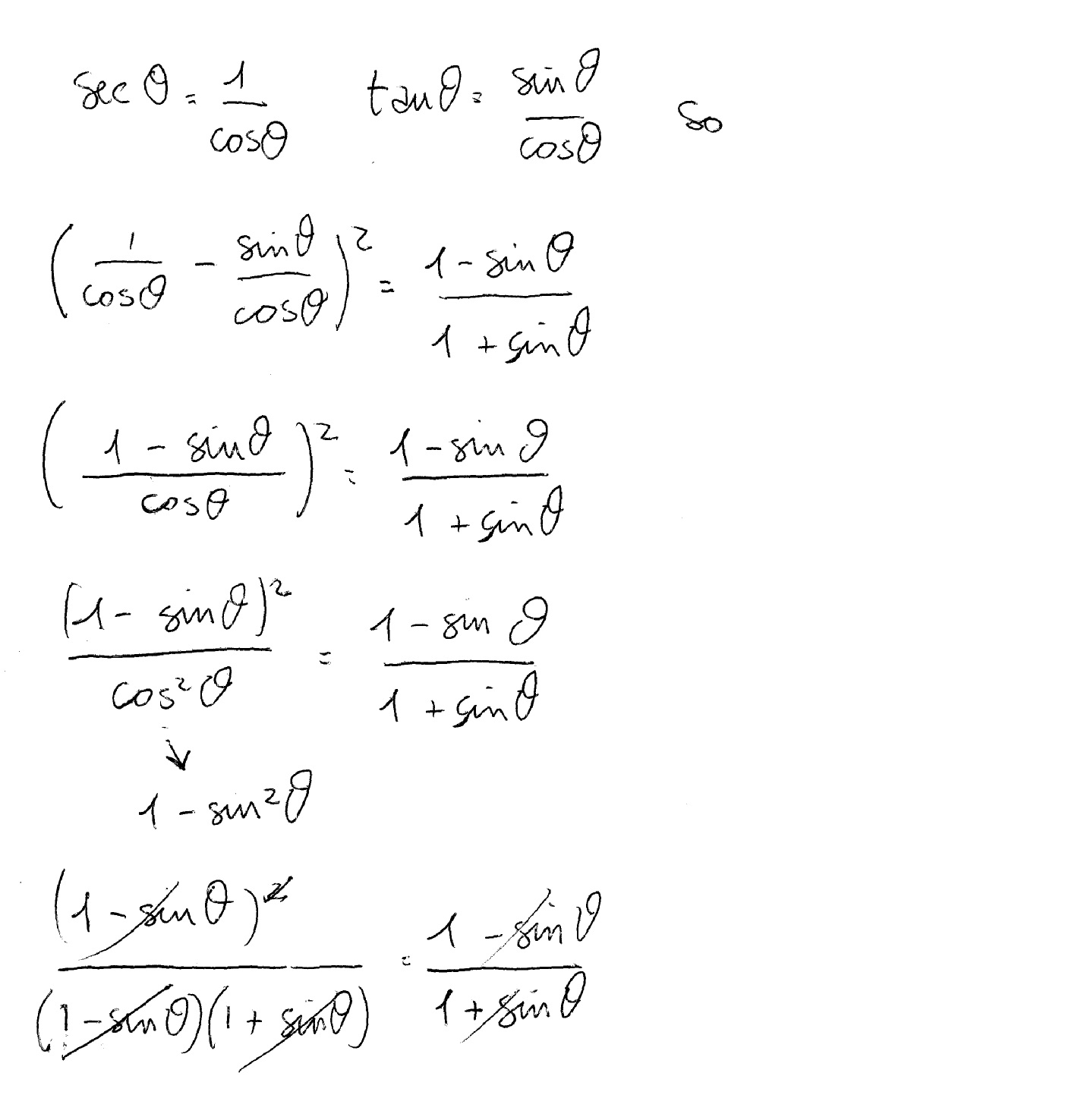


How Do You Prove The Identity Sectheta Tantheta 2 1 Sintheta 1 Sintheta Socratic



If Tan 2theta 1 2tan 2phi Then Show That Cos2theta Sin 2phi 0 Youtube
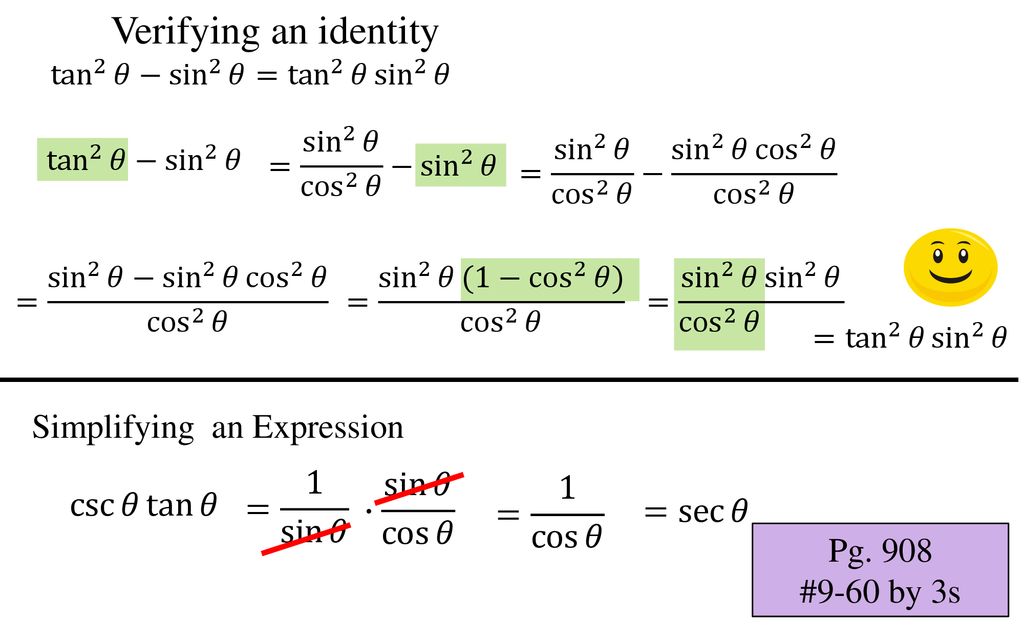


Trigonometric Identities And Equations Ppt Download



What Is The Value Of Sin 2theta 1 1 Tan 2theta


If Math 1 Sin 2 Theta 3 Sin Theta Cos Theta Math How Can We Prove That Math Tan Theta Frac 1 2 Math Quora



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Th



Viewcot 8 Cos 8 Sin 8 Pythagorean Identities Sin 2 8 Cos 2 8 1 1 Tan 2 8 Sec 2 8 1 Cos 2 8 Csc 2 8 Reflective



If Tan 2 Theta 1 2 Tan 2 Phi Prove That Cos 2 Phi 1 2 Cos 2 Theta Youtube



Prove That A Sin 2 Theta 1 Cos 2 Theta Tan Theta B 1 Sin 2 Theta 2theta Youtube
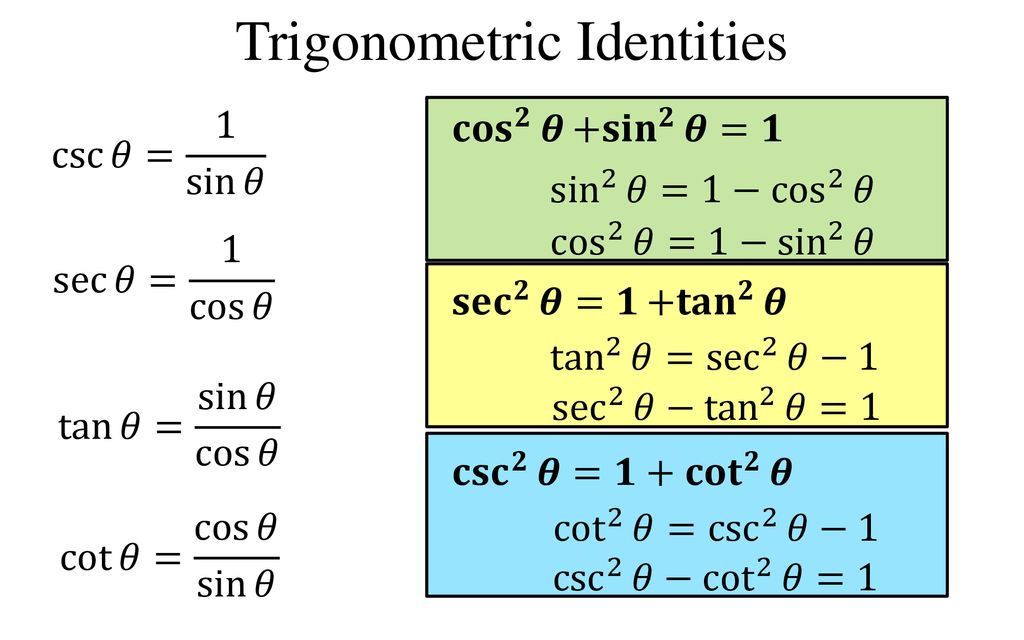


Trigonometric Identities And Equations Ppt Download


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora



Prove That Tan2 Theta Tan 2 Theta 1 Cosec 2 Theta Sec 2 Theta Cosec 2 Theta 1 Sin 2 Theta Cos2 Brainly In



Bysyyapnuctm5m



A Student Argues That Tan 2 8 1 Sec 26 Can Be C Gauthmath



16 Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta



5 1 5 2 Trigonometric Identities Ppt Download



Trigonometric Identities
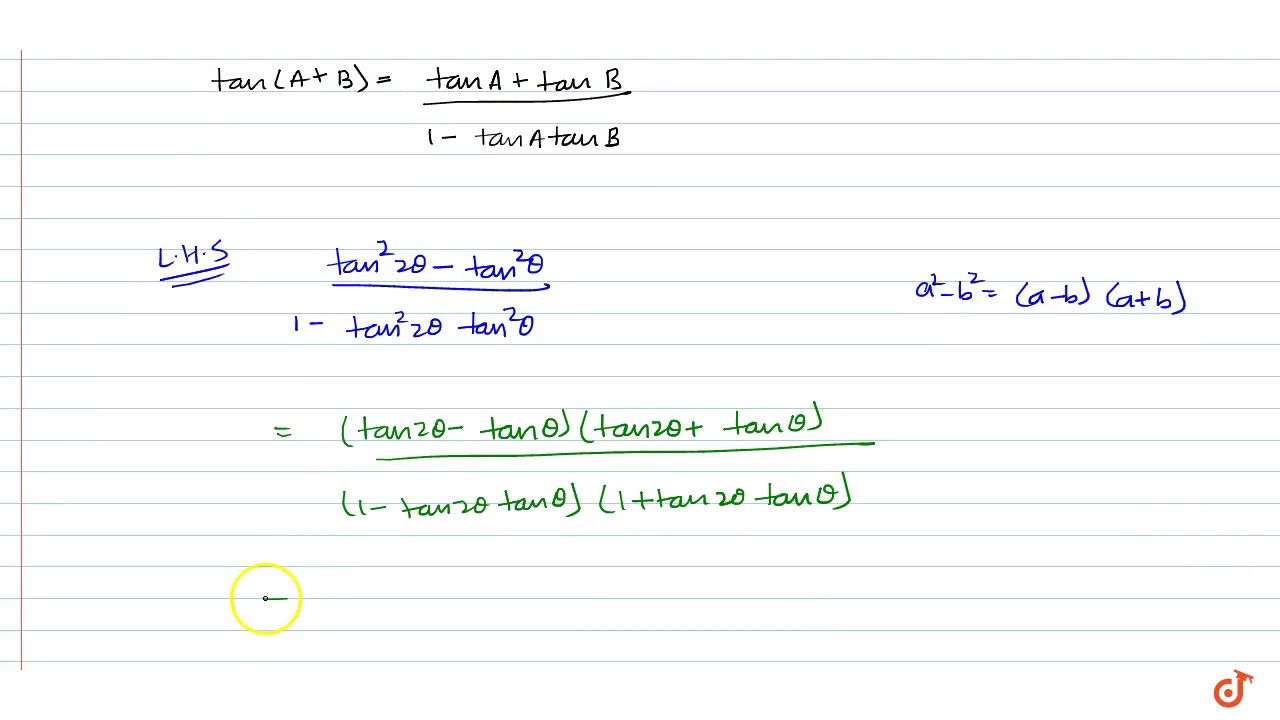


Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube
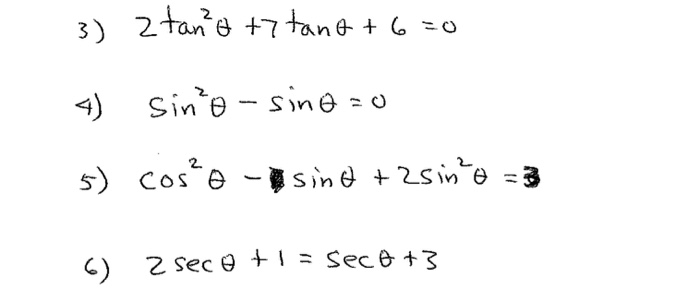


Solved 2 Tan 2 Theta 7 Tan Theta 6 0 Sin 2 Theta Chegg Com
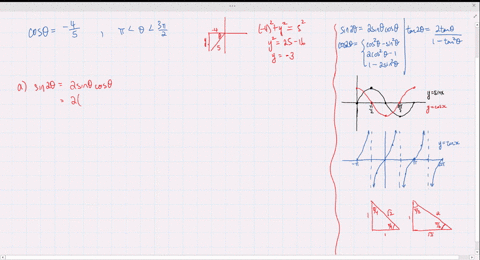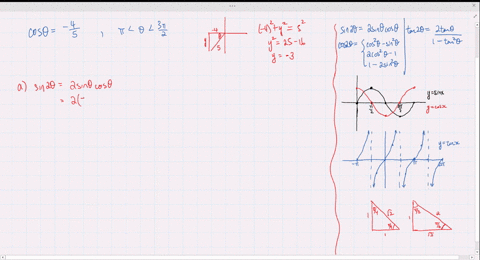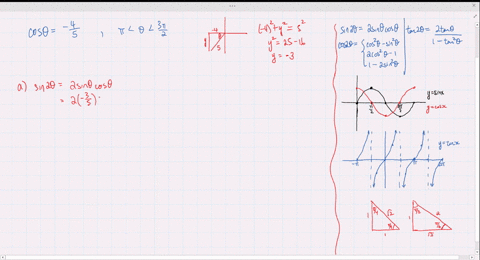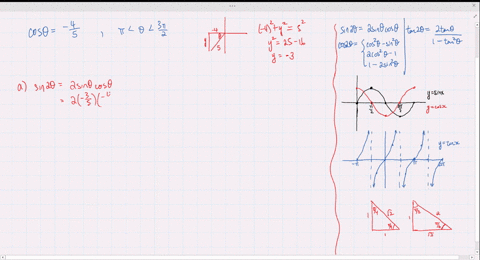


Solved Find The Exact Values Of Sin 2 Theta C



Prove That Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta


If Sin 4 Theta Sin 2 Theta 1 Prove That Tan 4 Theta Tan 2 Theta 1 Askiitians


